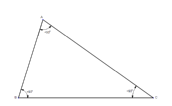
 | All angles are less than 90 degrees. | | |
| 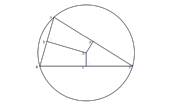 | The circumcenter is the intersection of the perpendicular bisectors of the sides. It is equidistant from all of the vertices. Note that the circumcenter may also be outside or on the triangle. | | |
|
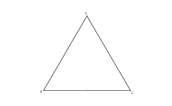 | All angles and sides are equal. | | |
| 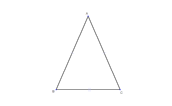 | At least two sides are equal. | | |
|
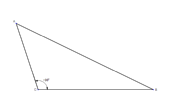 | One angle is greater than 90 degrees.
| | |
| 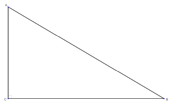 | One angle is 90 degrees. | | |
|
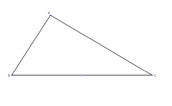 | All three sides are unequal. | | |
| 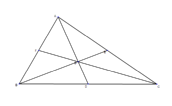 | The centroid is the intersection of all the medians. The centroid divides all of the medians in a ratio of 2:1. | | |
|
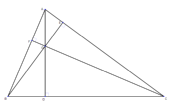 | The orthocenter is the intersection of the triangle's altitudes. An altitude is like a height of the triangle; it is perpendicular to a side and goes through the opposite vertex. | | |
| 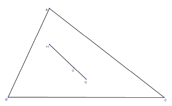 | The orthocenter, circumcenter, and centroid always lie on the same line. This line is called the Euler Line. | | |
|
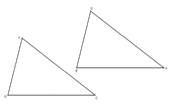 | If two triangles have three congruent sides, then the triangles are congruent. | | |
| 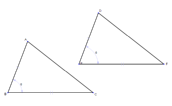 | If two triangles have two congruent sides and a congruent included angle, then the triangles are congruent. | | |
|
| |
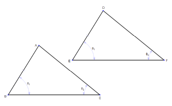 | If two triangles have two congruent angles and a congruent nonincluded side, then the two triangles are congruent. | | |
| 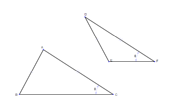 | If two triangles have two congruent sides and a congruent nonincluded angle, then they are not necessarily congruent. | | |
|
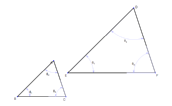 | If two triangles have three congruent angles, then they are not necessarily congruent. However, they will be similar. | | |
|  | Triangle with side angle side marked | | |
|
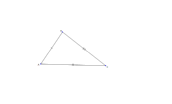 | Triangle with side-side-side marked | | |
| 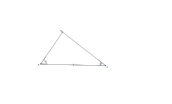 | Triangle with angle-side-angle marked | | |
|
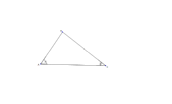 | Triangle with angle-angle-side marked | | |
| 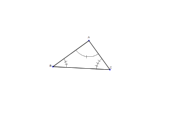 | This triangle shows markings for Angle-Angle-Angle. This is not a valid argument for congruence, but it does show similarity. | | |
|
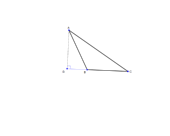 | An obtuse triangle with extended side is shown, but the diagram can be modified to form right and acute triangles as well. | | |
|  | 30-60-90 triangles are sometimes called half-equilateral triangles. | | |
|

